COURS 39/ La fonction différentielle
De par sa construction, un vérin est un récepteur asymétrique ayant des surfaces S1 et S2 différentes. Avec un débit identique pour la sortie comme pour la rentrée, la vitesse de sortie sera différente de la vitesse de rentrée.
Rappel des formules
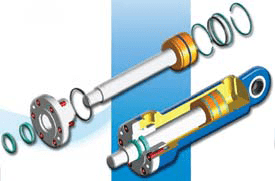
S1 : Surface côté fond
S2 : Surface côté tige
Surface fond : S1= πD²/4 =πr²
Surface annulaire : S2= (D²-d²)π/4
Vitesse de rentrée ou de sortie d’un vérin : V(m/s) = Q(l/min) / 6*S(cm²)
Sur certaines applications, il peut être intéressant de vouloir faire sortir et rentrer la tige d’un vérin à la même vitesse. Pour cela il existe plusieurs solutions :
→ Le vérin double tige
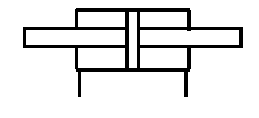Cette solution est la plus facile à mettre en oeuvre car, par construction, les deux surfaces S1 et S2 du vérin sont identiques.
Inconvénients : son encombrement et son coût.
→ Le compensateur de débit
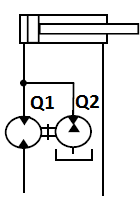Il est dimensionné tel que S1/S2 = (Q1+Q2)/Q1. Il sera difficile de trouver des ratios de débit correspondant au ratio des surfaces si il est différent de ½. Sa mise en
oeuvre peut s’avérer difficile et occasionne des pertes de charge importantes. Il possède néanmoins l’avantage de pouvoir être monté sur un circuit fermé.
→ Le montage différentiel
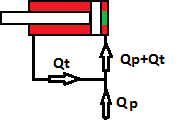Il est facile à mettre en oeuvre.
Il consiste, pour une sortie de tige, à cumuler le débit refoulé par la chambre annulaire Qt avec le débit principal Qp.
Ainsi, le débit reçu côté fond Qf sera égal à : Qf=Qp+Qt
Le volume d’huile expulsé côté tige Qt étant réinjecté côté fond, la vitesse de sortie de tige sera donc égale au débit principal Qp appliqué sur la seule surface de
tige (en vert sur le schéma).
Nous avons donc les équations de vitesses suivantes :
Vrentrée = Qp / 6 * S2
Vsortie = Qp / 6 * (S1 – S2)
→ Avec S1-S2 égale à la surface de la section de la tige :
Dans cette configuration, si notre vérin est choisi tel que S2/S1 = 1/2 (soit S1=2*S2) nous obtenons donc les vitesses suivantes :
Vrentrée = Qp / 6 * S2
Vsortie = Qp / 6 * ((2*S2)-S2)
Vsortie = Qp / 6 * S2
Vsortie = Vrentrée
De même, l’effort F développé en sortie de tige sera donc uniquement le produit de la pression appliquée sur la surface égale à celle de la section de tige ; les
pressions appliquées sur les surfaces annulaires s’équilibrant, comme sur le schéma ci-dessous :
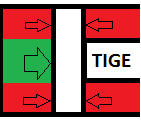
F = P / (S1-S2)
Variantes de construction
→ à l’aide d’un sélecteur de circuit (gros débit) sur la canalisation côté tige et d’un distributeur classique 4/3 :
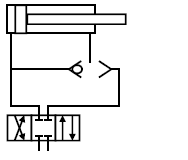
→ à l’aide d’un distributeur 4/3 possédant directement une position différentielle sur la position de sortie :
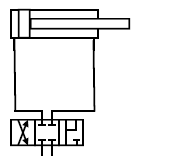
→ à l’aide d’un distributeur 4/3 centre ouvert, en reliant le côté tige non pas sur un des deux orifices de sortie, mais directement sur le refoulement de pompe :
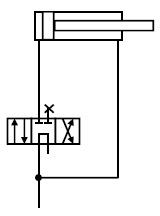
Conclusion
Ce type de montage est facile à mettre en oeuvre pour réaliser une sortie de tige rapide avec des efforts réduits. On trouvera donc également une application pour les machines ayant des approches rapides en mode différentiel pour finalement terminer la course de sortie en mode « normal » afin de pouvoir bénéficier, à une vitesse plus faible, d’un effort maximal.
